

Definition: A hypermaze is a Maze in a higher dimension. A hypermaze is more than just what is normally considered to be a "3D Maze". A standard 3D Maze has passages like any other, just that they tunnel through a 3D solid instead of move across a 2D surface. A hypermaze however is a true multidimensional Maze, and increases the dimension of the solving object and the passages themselves. In a normal Maze you move a point through it, and the path behind you forms a line. In a hypermaze you move a line through it, and your path forms a surface!
Dimensions: In general, for any Maze, be it a standard Maze or a hypermaze, the solution is represented by an n-dimensional figure. That n-dimensional figure is formed by moving an (n-1)-dimensional object along the solution path. The environment forming the Maze itself is a (n+1) or higher dimensional object. For example, a standard non-hypermaze consists of moving a 0D object (a point), along a 1D solution path (a line), through a 2D or higher dimensional environment (a plane, solid, etc). In a hypermaze you move a 1D object (a line), along a 2D solution path (a plane), through a 3D or higher environment (a solid, 4D solid, etc).
Hyperhypermazes: Hypermazes can be more than just moving a line. A hyperhypermaze increases the dimension of the solving object and the solution path again. In a hyperhypermaze, you move a 2D plane through a 4D or higher dimensional environment, and your path forms a 3D solid. A hyperhypermaze can be considered a hypermaze of the 2nd order. A hypermaze of the 3rd order is even more extreme, involving moving a 3D universe or hyperplane through a 5D environment or beyond, forming a 4D solution path! A normal hypermaze is a hypermaze of the 1st order, while a standard Maze involving moving just a point is a non-hypermaze, or a hypermaze of the 0th order.
Physical model: In solving a non-hypermaze, you work with what amounts to a point, such as a marble, a cursor, or yourself. In solving a hypermaze, you work with a line, such as a long section of string. You grab and drag different parts of the string, moving it up and down and back and around past the obstacles in the hypermaze. Note the solving line in a hypermaze needs to act like an infinitely long line, or rather you shouldn't be able to retract the ends of the line to inside the hypermaze. A mere line segment would be equivalent to a non-hypermaze, because you can just crumple the section of string into a ball, and then move the point through like in a non-hypermaze. As you move the line into the entrance face of the 3D hypermaze object, through the hypermaze across to the exit face, the ends of the line should stick out both adjacent faces. This can be modeled by an infinite line without endpoints, or a finite line segment where the ends are tied to points outside the hypermaze. A example physical model of a hypermaze is a 3D construct in the middle of a room. A piece of string has ends attached to opposite walls of the room. You then have to move the middle part of that string into one side of the 3D solid and out the other.
Entrances: The entrance and exit to a non-hypermaze is a point. The entrance and exit to a hypermaze is of course a line. Multiple entrances on the face of a 3D non-hypermaze consist of a set of points, like a piece of Swiss cheese. Multiple entrances on the face of a hypermaze consist of crisscrossing lines, like the canals on the surface of Mars. Note the outer surface or any cross section of a hypermaze can form a non-hypermaze. In a 2D non-hypermaze, a solution path starting on one edge and ending on another splits the walls into two halves. In a 3D hypermaze, a solution surface starting on one face and ending on another again splits the solid into two halves. In the physical model above, the hypermaze could rest on a table, however the top half needs to be suspended from the ceiling, since the solution technically cuts it into two pieces with space between them.
Obstacles: A model of a hypermaze can have relatively sparse obstructions and still be challenging. This sparseness can allow a physical model to actually work where one can reach inside the solid at points to manipulate the string. A non-hypermaze (especially in 3D) needs to be relatively solid, i.e. basically needs to be formed of tunnels, because there are so many places a point can fit. A "passage" for a hypermaze line to follow needs to at least be a plane area, like a low ceiling warehouse or the area behind a bookcase. Note a "dead end" in a hypermaze can be a mere column in the middle of a room, and doesn't need to have walls all around, in which 1D "tentacles" or lines are enough to obstruct and form dead ends for the solving string. Picture a parking garage with a concrete column down the middle, and you're walking a dog, where the leash connecting you and the dog is part of the hypermaze solving line. If the dog goes around one size of the column and you go around the other side, then the line gets caught on the column, and column stops you from getting across the room. If however the column is like a lamppost instead of connected to both floor and ceiling, then you can throw the leash over the top of the pole and keep going. For another example, picture an upright letter "F" attached to the floor, between a floor and ceiling, while the solution string approaches it from the right. If the string goes between the two horizontal tines of the "F", or between the bottom tine and the floor, then it will get caught on the stem of the "F", and that will act like a dead end for that section of the string (the proper path goes over the top of the "F").
Obstacle formula: More generally, for any Maze or hypermaze, the dimension of the obstacles needs to be at least (dimension of environment) - (dimension of solving object) - 1. For example, for a standard non-hypermaze in 2D, you need at least 1D lines to obstruct (i.e. form tunnels and dead ends for) a 0D solving point in the 2D environment. For a non-hypermaze in 3D, you need 2D surfaces to obstruct (i.e. form tunnels and dead ends for) a 0D solving point in the 3D environment. For a hypermaze in 3D (our example here) you need at least 1D lines to obstruct (i.e. form places to get caught on) a 1D solving line in the 3D environment. For a hyperhypermaze in 6D, you need 3D solids to obstruct a 2D solving surface in the 6-dimensional environment. And so on.
Alternate model: In addition to an infinite line, another model that works for a hypermaze line is an elastic circle or ring. The entrance and exit are ring shaped holes in the sides of the hypermaze object, with at least one wall in the middle of the ring preventing you from collapsing the ring to a point. You then move the ring down the "rail", stretching and compressing its circumference as appropriate. In this model, the hypermaze is divided into two pieces by the solution - one piece for the outer Maze and one piece for the part inside the ring, where the inner piece needs to be suspended in air, e.g. held at the right point with wire or whatever in a physical model. Note in all general hypermazes, the solving line is completely elastic, so can be stretched and bent around any obstacle to form an arbitrarily curved solution surface. Of course there are many possible variant rules one can add to a hypermaze for extra challenge, such as one where the solving string can't be bent beyond some radius "r".
Example models: In the hypermazes pictured here, there's a ceiling floating above a foundation. From the ceiling "stalactites" dangle down, and from the floor "stalagmites" grow up, and they branch and twist around in a complex fashion like a briar patch. The hypermaze consists of two separate solids, just as how in a 2D non-hypermaze, with the entrance on one side and the exit on the other, the solution path divides it into two separate shapes. Your goal is to move string between the floor and ceiling, in one side and out the other, like a piece of dental floss. Note for hypermazes of this model, it doesn't matter which side you enter. You can enter from the north face and exit on the south or vice versa, you can enter from the west face and exit on the east or vice versa, or you can make the string enter at a corner.

Small example: Above is a perspective rendering of a simple 9x9x9 cube hypermaze. Note the Maze is reasonably sparse, where there are places you can see through and out the other side. If you were to start by moving the string in from the leftward (dark red) face, note that there are 5 possible ways of entering. The row across the very bottom is one, and there are four possible combinations in the upper half. If you were to start by moving the string in from the rightward (pink) face, there are 2 possible ways of entering. The row across the very top is one, and the path from upper left to lower right is the other.

Solution coloring: Above is another rendering of the same 9x9x9 cube hypermaze, viewed from the opposite corner. Here everything connected to the base is colored blue, while everything connected to the ceiling is red. This is somewhat of a spoiler or a solution to the hypermaze, because to solve it you just need to have all parts of the string between a red and blue section at all times. (A similar method works to solve 2D non-hypermazes, if you color the walls on one half a different color from those in the other half.) Note the red pole surrounded by blue near the bottom of the left hand face. Part way through solving, you'll need to loop the string out and around that red pole, like throwing a rope over the top of a lamppost.

Large example: Above is a orthographic rendering of a very complex hypermaze (73x73x73 cubes). Note there's literally billions of ways of arranging the string across and moving it into one of the hypermaze's faces. Because this is a "perfect" hypermaze, only one solution and hence initial starting configuration actually works! And that's just to get started, much less to actually navigate through the hypermaze.
Solution half: Above is a picture of just the bottom half piece of the same 73x73x73 hypermaze, with the top half removed. This exposes the solution similar to how different coloring does, in which the solution surface always follows between the area removed and the area still present.
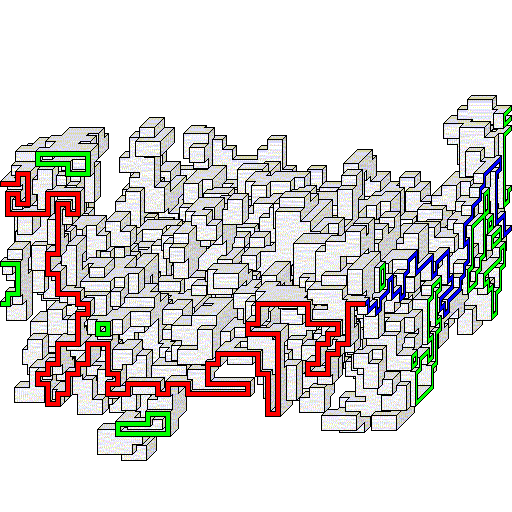
Solution surface: Above is the unique solution to the 73x73x73 hypermaze, showing the complex solution surface, or the path taken by the string. The edge colored in red is the edge of the surface, i.e. the entrance line that the string must enter (no other combination works) if you enter via this face, or the exit line that the string leaves from if you exit via this face. The edge colored in blue is the same entrance/exit line along the adjacent face. Note there are some holes in the surface, whose circular edges are colored green. These are places where the solution surface goes back to and briefly touches a boundary face (like the red pole in the earlier example). This is just a rendering effect to show the solution surface clipped to the boundary of the hypermaze itself, in which the actual solution surface of course has no holes. Note the green figure-8 shaped circuit near the far right edge. That shows an interesting point where two such holes touch. A hypermaze solution surface will never actually intersect itself, but it can briefly touch itself at various points, where some areas may need to be passed through by the solving line more than once. The analogy here is having your thumb and forefinger form a circle, almost touching, where to move the solving line over a solution surface formed by your fingers, it requires moving the line through the narrow space between the fingers twice.
Hypermaze duals: The passages in a 3D non-hypermaze are similar to the walls in a 3D hypermaze. Basically, a 3D non-hypermaze and a 3D hypermaze are duals of each other, where turning all barriers into open space and vice-versa turns one into the other! Ok, there's a slight difference, because a standard 3D non-hypermaze consists of a single connected tree, while a 3D hypermaze has two separate trees attached to boundary surfaces. In the hypermaze graphics pictured, you can treat the wall blocks as passages, and attempt to find a path from the top face to the bottom face. The dual of a Maze is basically the dual of its graph, with the new passages being the old walls and vice versa. A good example of that is this 2D non-hypermaze. Normally black is wall and white is passage, and your goal is to navigate from the top to bottom. However you can also try to solve the dual, and treat white as wall and black as passage, and your goal is to go from the left edge to the right edge.
Solving the dual: For any Maze or hypermaze, if it has a solution, then its dual has no solution. In the example 2D Maze, if there's a white path connecting top to bottom, then there can't also be a black path connecting side to side, and vice versa. Similarly for the 3D hypermaze, if you can follow a solution surface through the solid, which splits the environment into two pieces, then that means the dual 3D non-hypermaze is unsolvable, since there's no path from the top wall to the bottom wall. The reverse is of course true too, where if there's a path connecting the top wall to the bottom wall, then the hypermaze is unsolvable, because there's no way to run a solving line through the solid without getting caught on the column connecting the two halves. In a 2D Maze, it's always the case that either the Maze is solvable or its dual is solvable. However in a 3D environment, it's possible that neither Maze is solvable! Consider a hypermaze where the top and bottom halves are separate, but linked like a chain. In such a case the 3D non-hypermaze is unsolvable, because there's no way to get from the top to the disconnected bottom. However the hypermaze is also unsolvable, because there's no way to run a length of string between the two halves, because they're inseparably linked.
Dual formula: The general rule is for a hypermaze of order "p" in a n-dimensional environment, its dual is a hypermaze of order (n-p-2). For example, in a 2D environment, the dual of a non-hypermaze (order 0) is another non-hypermaze (2-0-2 = 0), as seen in the 2D example above. In a 3D environment, the dual of a standard hypermaze (order 1) is a non-hypermaze (3-1-2 = 0) and vice versa, as seen in the 3D example above. The dual of the tunnels forming a 4D non-hypermaze is a hyperhypermaze (4-0-2 = 2nd order hypermaze), which you should be able to run a solving plane through forming a solution solid.
Creation algorithm: The ability to create 3D hypermazes is in the latest versions of the Maze program Daedalus. All hypermazes on this page were created and rendered by the program. The algorithm for creating a hypermaze turns out to be pretty simple. Start with the top and bottom floors, and then grow a bunch of random wall branches from them like a tree, where each appended branch connects to an existing object at exactly one end. This is exactly the same as how one adds walls to a 2D non-hypermaze when creating a Maze by adding walls, which also simultaneously grows two trees of walls inward from the boundaries. Creating hypermazes is also similar to how one carves the tunnels in a 3D non-hypermaze, with the only difference being that the tree structure in a hypermaze forms walls instead of the passages, and in a hypermaze you grow two trees simultaneously. These hypermazes are "perfect", in that there's exactly one solution surface, just as how a perfect non-hypermaze has exactly one solution path and exactly one path from any point in the Maze to any other point.
Solving algorithm: The ability to solve hypermazes is also in the latest versions of Daedalus. To solve a hypermaze means finding its solution surface. The solution surface can be generated by focusing on the different solids that compose the hypermaze, similar to coloring them differently as described earlier. For any two adjacent bits of obstacle with unbroken space between them, if the two bits are part of the same solid, then connect them. This fills in all the false areas, leaving just the cracks between separate solids. For a perfect hypermaze, the space left will be exactly the solution surface. This solving method works similar to the method of solving a standard non-hypermaze by filling in all the dead ends. Although more technically, solving hypermazes is a 3D version of the "blind alley sealer" solving algorithm, which also works by adding connections between contiguous areas of the Maze.
State: Hypermazes are special because they go beyond having an easily definable state. Most Mazes (and puzzles in general) tend to have a finite number of easily enumerable states, and a small number of actions you can take at any one state, i.e. the decision tree is defined by a simple graph. This is true regardless of the type of Maze, and it covers almost all logic Mazes or Mazes with special rules, where I call this concept Maze equivalence. For example in a 10x10 orthogonal passage 2D Maze, there are 100 possible locations where the solving point can be, and in any cell you have up to four choices you can take to visit neighboring cells. However in a hypermaze represented by a 10x10x10 arrangement of blocks, there are virtually an infinite number of combinations of how the solving line can be spread out through it, and ways in which you can manipulate the string at any one configuration, just as there's virtually an infinite number of ways you can run a length of string through a room. It's easy to count and enumerate all the states of a non-hypermaze. Although the states of a hypermaze are still ultimately finite, an analogy is that a non-hypermaze is "countable" like the set of integers in a range, while a hypermaze is "uncountable" like the set of real numbers in a range.
Interface: Because hypermazes are fundamentally different from other Mazes and state based puzzles, there's a lot of potential to make interesting new computer or physical puzzles involving hypermazes. The most challenging aspect of hypermazes is easily interfacing with them. A computer interface to navigate a hypermaze is challenging to make, since you need to be able to look at all parts of the line, and the nearby parts of the hypermaze in the 3D environment, and be able to select and drag different parts of the line, and hopefully the line acts like a real string where points near the grab point get partially dragged too. A physical model of a hypermaze is also challenging to make, because the model is delicate yet needs to be rigid, and it tends to defy gravity.
Philosophy: A hypermaze is interesting because your focus is not on a single point, or on your individual self, but is rather across multiple points, in which you need to deal with every point along a line at once. Similarly in life one can think for just themselves, or can work for the environment and serve the world as a whole. :-) An interesting team building exercise would be a large physical hypermaze, in which the line consists of people tied along a rope at different points, and they all need to cooperate and move together to get through!