
In astrology, the "best" system of house division is highly debatable. Many different house systems have been proposed over the centuries, and some have become popular. Of course, just because a system is old or popular doesn't necessarily make it better, any more than being new or less common makes a system worse. One way to define "best" is the most astrologically accurate, which is one reason why I respect Topocentric (Polich-Page) houses, because at least according to Wikipedia it was determined "by observing events in people's lives and assessing the geometry of a house system that would fit." However, until detailed studies are done and proof is found, the astrologer must base house division on what sounds right based on a description of the system, or what looks right based on visual placement of the house cusps.
House systems are a way of dividing the local horizon into the twelve zones or houses. Each house covers 30 degrees on average, however the Earth's tilt to the ecliptic among other things can make them vary. There are two main points which are clearly defined without ambiguity: the Ascendant (Asc) and the Midheaven (MC). Most house systems are quadrant based, which means the angles are fixed: The 1st house is the same as the Asc, and the 10th the same as the MC. (Some, such as Equal house systems, can disassociate these points from each other.) Most of the differences between house systems start when placing the eight remaining "minor" cusps. Not counting opposing cusps, we have to determine where to place four points on the zodiac. The Asc and MC are usually about 90 degrees apart from each other, although they may range anywhere from 0 to 180 degrees apart.
The simplest quadrant based house system is Porphyry, which simply trisects each quadrant equally. A subset of quadrant systems is graduation house systems. Graduated houses have house sizes vary more gradually, by making the center house in the small quadrant narrower, and the center house in large quadrants wider. In other words, their math is entirely based on the ecliptic, and doesn't involve other components not related to the difference between the Asc and MC. "Sinusoidal" can be considered a subclass of graduation house systems, in that its graduation is based on a sine curve. A sine wave (and all its derivatives, to use a term from calculus) is eternally smooth, which avoids any "discontinuities" around the circle of houses. Therefore, Sinusoidal can make its own argument for why it could be considered the "best" house system, or at least "best looking" system when displayed in chart wheels.
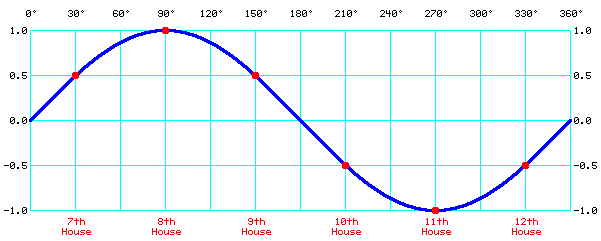
From the most compressed house in the smaller quadrant, to the most expanded
house in the larger quadrant, is four houses or sizes, which can plot four
points on a sine wave. Given that one end (the bottom of the sine wave) is
sin(-90) = -1.0, and the other end (the top of the sine wave) is sin(90) = 1.0,
then the other two houses between them are sin(-30) = -0.5 and sin(30) = 0.5,
as seen in the sine wave diagram. Although the
four numbers (-1, -0.5, 0.5, 1) are taken from a sine wave, they're simple and
don't require trigonometry to calculate. They can also be proportioned and
expressed as (0, 0.25, 0.75, 1) or (0, 1, 3, 4).
The calculations for Sinusoidal house systems are also based on the sine wave.
That means the relation of the sizes of houses 11-8 (most narrow to most
expanded) plot four points upon a sine wave. 11th house is sin(-90) = -1.0 or
the bottom of the wave, while 8th house is sin(90) = 1.0 or the top of the
wave. That makes 10th house sin(-30) = -0.5, and 9th house sin(30) = 0.5.
That's gives a distribution of (-1, -0.5, 0.5, 1) or (0, d, 3d, 4d) which seems
simple but is still based on the trigonometry of a sine wave. There's more than
one potential way to apply a sine wave to house sizes. Below are two specific
Sinusoidal house systems:

Sinusoidal Delta is a house system in which the differences between adjacent house sizes form a sine wave. That means subtracting house sizes, in which plotting the differences between the sizes of houses 11, 10, 9, and 8 will always form a sine wave. If (10th size-11th size) is n, then (9th size-11th size) is 3n, and (8th size-11th size) is 4n. This is summarized in the chart below:
"Sinusoidal Delta" (formerly "Neo-Porphyry") Houses.
Asc 12th 11th MC 9th 8th 7th
| | | | | | |
+----------+----------+----------+----------+----------+----------+
^ ^ ^ ^ ^ ^
angle angle angle angle angle angle
x+n x x+n x+3n x+4n x+3n
Note that for all quadrant sizes >= 30 degrees, (10th size - 11th size) = "n", and also (8th size - 9th size) = "n" as well, which ensures houses within the large and small quadrants always have the same differences with respect to each other. Just as important, (9th size - 10th size) = 2n, which ensures the two houses on either sides of angles also have the same differences with respect to each other. Subtracting any two house sizes always gives multiples of (0, 1, 2, 3, or 4) with respect to "n", which means these offsets give a consistent "smooth" sine wave look around the entire wheel. Examples of Sinusoidal Delta at different latitudes can be seen in the left hand column of the picture above.
Computation: The unique values for "n" and "x" can be computed based on the small quadrant size "q", given the equations (x+n) + x + (x+n) = q, (x+3n) + (x+4n) + (x+3n) = 180-q. There are two equations and two unknowns, both in terms of q. These equations are relatively simple, with the solution: n = (90 - q) / 4, x = (q - 30) / 2.
Limitations: Sinusoidal Delta doesn't work when the small quadrant is < 30 degrees. That means when MC-Asc < 30 degrees or > 150 degrees. If the large quadrant is 5x the size of the small quadrant, then no positive value of "x" will allow the small 10th house to be x+n, and the much larger 9th house be x+3n. Therefore in Sinusoidal Delta houses, when the small quadrant reaches 30 degrees, it pinches the 11th house to zero size. Less than 30 degrees, there's no longer any way to make the 10th house be x+n and the 9th house be x+3n (at least not without introducing the weird concept of negative sized houses). Therefore implementation should just bisect the narrow quadrant (keeping the 11th house 0 sized) for all quadrants < 30 degrees. That allows the system to produce usable results for all charts. The house size differences no longer fit the sine wave model (because they can't in such scenarios) but that's the best one can do without falling back to a different system. For this reason, I consider the newer Sinusoidal Ratio house system below to look better and be an improvement upon this system.
Naming: Given the tradition and standard of naming most house systems after their inventor or popularizer, this house system is best called "Pullen (Sinusoidal Delta)", or abbreviated "Pullen (SD)" or "Pullen (S-Delta)". Originally this system was called "Neo-Porphyry", because it was an early form of quadrant trisection that's more graduated than Porphyry's simple equal trisection. Similarly, certain versions of the Kepler and Sirius astrology programs called it "NeoPorph". However, this name isn't the best, because the house system isn't directly related to Porphyry houses or the work of Porphyry of Tyre.
History: Sinusoidal Delta houses were first conceptualized and implemented by Walter D. Pullen in the evening of Feb 13, 1994, and first described on Feb 21, 1994 in an article posted to Usenet newsgroup alt.astrology. They've been available in every version of Astrolog since 4.10, are in other astrology programs such as Kepler and Sirius, and may also be selected online in Astro.com charts.
It's possible to do other than simply add sine wave offsets to houses (the Sinusoidal Delta house system above). Instead, we can proportion or ratio the entire house sizes themselves to each other based on the sine wave constants, or multiply instead of add. That results in using a "sinusoidal ratio" instead of a "sinusoidal delta", hence the general name "Sinusoidal Ratio houses". As before, let "x" be the smallest house in the compressed quadrant (assume the 11th). There's a ratio "r" multiplied by it to get the slightly larger 10th and 12th houses. The value "r" starts out at 1.0 for 90 degree quadrants, and gradually increases as quadrant sizes differ. Houses in the large quadrant have "r" multiplied to "x" 3 times (or 4 times for the largest quadrant). That results in the (0r, 1r, 3r, 4r) distribution from the sine wave above. This is summarized in the chart below:
"Sinusoidal Ratio" Houses.
Asc 12th 11th MC 9th 8th 7th
| | | | | | |
+----------+----------+----------+----------+----------+----------+
^ ^ ^ ^ ^ ^
angle angle angle angle angle angle
rx x rx (r^3)x (r^4)x (r^3)x
Note that for all quadrant sizes, (10th size / 11th size) = "r", and
also (8th size / 9th size) = "r" as well, which ensures houses within
the large and small quadrants always have the same proportions to each other.
Just as important, (9th size / 10th size) = r^2, which ensures the two houses
on either sides of angles also have the same proportions to each other.
Dividing any two house sizes by each other always gives powers of (0, 1, 2, 3,
or 4) with respect to "r", which means these proportions give a
consistent "smooth" sine wave look around the entire wheel regardless
of quadrant size. Examples of Sinusoidal Ratio at different latitudes can be
seen in the right hand column of the picture above.
I like the results, and to me it accomplishes the intent of a
"smooth" look even better than Sinusoidal Delta.
Computation: The unique values for "r" and "x" can be computed based on the quadrant size "q", given the equations rx + x + rx = q, xr^3 + xr^4 + xr^3 = 180-q. There are two equations and two unknowns, both in terms of q. The solution is semi-complex (especially given the polynomial cubic and quartic terms), however the full solution is available (which does show the trivial integer solution of q=90, x=30, r=1). It's also possible to binary search to solve for "r" empirically. Given a candidate for "r", compute "x" given 1st equation: x = q / (2r + 1), then compare both against 2nd equation: 2xr^3 + xr^4 = 180-q, to see whether current "r" is too large or small.
Limitations: None, as the Sinusoidal Ratio house system works for all charts and quadrant sizes. In the degenerate case when Asc=MC, the three houses in the small quadrant will be 0 size (as they will be for any quadrant based house system). To do otherwise means that means that Asc != 1st and/or MC != 10th, which may cause other problems or at least break assumptions about that house system. However, houses 7 and 9 should also be 0, and house 8 180 degrees. As the small quadrant approaches 0, the 8th house approaches 180 degrees. In the formulas, that means x=0 and the ratio "r" approaches infinity.
Naming: Given the tradition and standard of naming most house systems after their inventor or popularizer, this house system can be called "Pullen (Sinusoidal Ratio)", or abbreviated "Pullen (SR)" or "Pullen (S-Ratio)".
History: Sinusoidal Ratio houses were conceptualized and first implemented by Walter D. Pullen in the evening of Jan 22, 2016. This came about in discussions on the Swiss Ephemeris Yahoo group with Alois Treindl and others about if there was a better way to approach Sinusoidal houses that doesn't have the limitations of Sinusoidal Delta. Sinusoidal Ratio houses are implemented in Astrolog 6.10 and beyond, and may also be selected online in Astro.com charts.